About Me

I am a computational physicist specializing in materials modeling, data-driven simulation, and quantum system dynamics. My research integrates physics-based theory with high-performance computing and machine learning to address challenges in materials reliability, defect behavior, and electronic transport. Currently pursuing a Ph.D. in Physics at Oklahoma State University, I focus on simulating non-equilibrium phenomena in quantum spin systems, predicting threshold displacement energies in radiation environments, and modeling defect-limited transport in disordered two-dimensional materials. I also work on device-level simulations to optimize perovskite solar cells for high-efficiency and space-resilient applications. With a passion for bridging theory and application, I aim to contribute to advances in materials design, semiconductor device engineering, and predictive modeling for emerging technologies.

Technical Skills

Programming & Scientific Computing: Python, C++, Mathematica, MATLAB, Bash/Shell scripting
Numerical Modeling: Differential equation solvers, Fourier transforms, and time-evolution algorithms
High-Performance Computing (HPC): Experience with HPC clusters, batch scheduling systems (Slurm), parallelization concepts (MPI), job automation
Data Science & ML: Scikit-learn, NumPy, SciPy, Pandas, Matplotlib, Seaborn, symbolic regression, feature extraction, compressed sensing
Materials Modeling Tools: DFT, molecular dynamics, UCSF ChimeraX (molecular visualization)
Development Tools: Git, Jupyter Notebooks, Microsoft Excel, Latex

Featured Research Projects

1. Machine Learning-Driven Analytical Models for Materials Science

1.1 Machine Learning-Driven Analytical Models for Threshold Displacement Energy Prediction in Materials

Understanding how materials respond to radiation is crucial for applications in nuclear reactors, spacecraft, and radiation shielding. The threshold displacement energy (Ed), which quantifies the minimum energy required to create a stable defect in a material, plays a key role in predicting radiation damage. However, conventional methods to determine Ed rely on expensive experiments and computationally intensive simulations. In this work, we leverage the Sure Independence Screening and Sparsifying Operator (SISSO) machine learning algorithm to develop analytical models for predicting Ed using fundamental material properties. Our models achieve high accuracy for monoatomic materials, outperforming existing empirical approaches. While predictions for polyatomic materials reveal challenges due to data complexity, they highlight opportunities for further improvements with expanded datasets. A key finding of our study is the identification of cohesive energy and melting temperature as dominant factors influencing Ed, providing insights into defect formation and material resilience. By offering a data-driven approach to estimating radiation damage, this work lays the groundwork for accelerated material screening and design in radiation-hardened environments.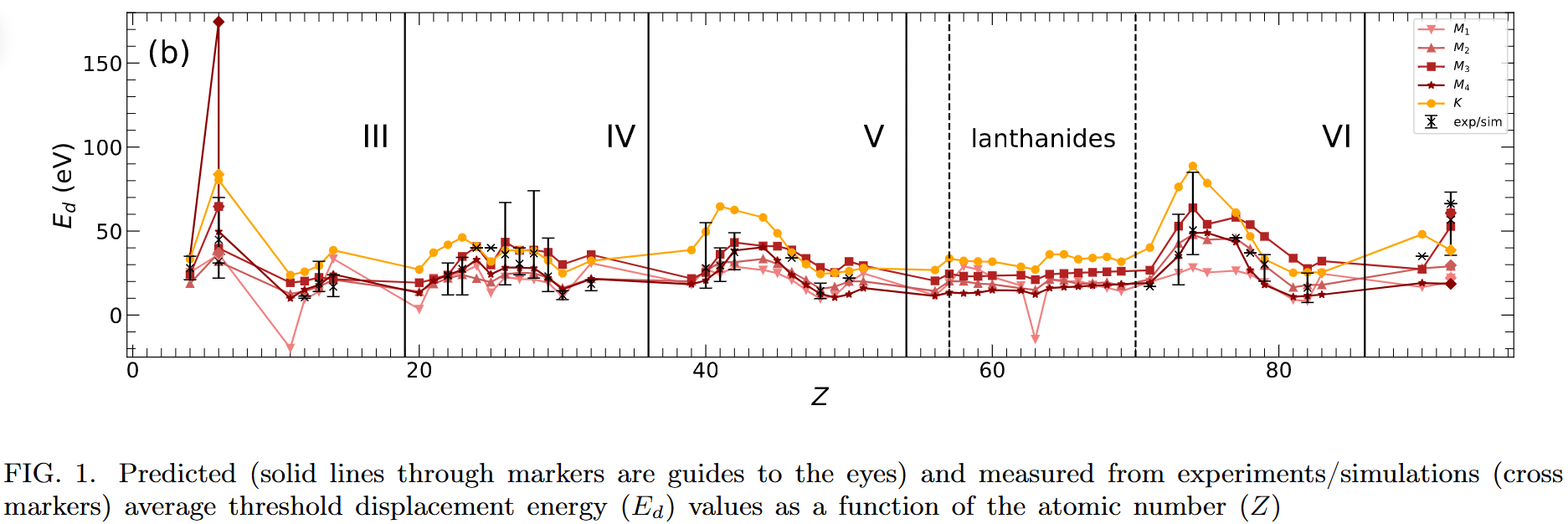

2. Quantum Simulation and Quantum-Enhanced Sensing

2.1 Heisenberg-limited entanglement generation in spin-1/2 XXZ models using Floquet engineering for quantum-enhanced sensing

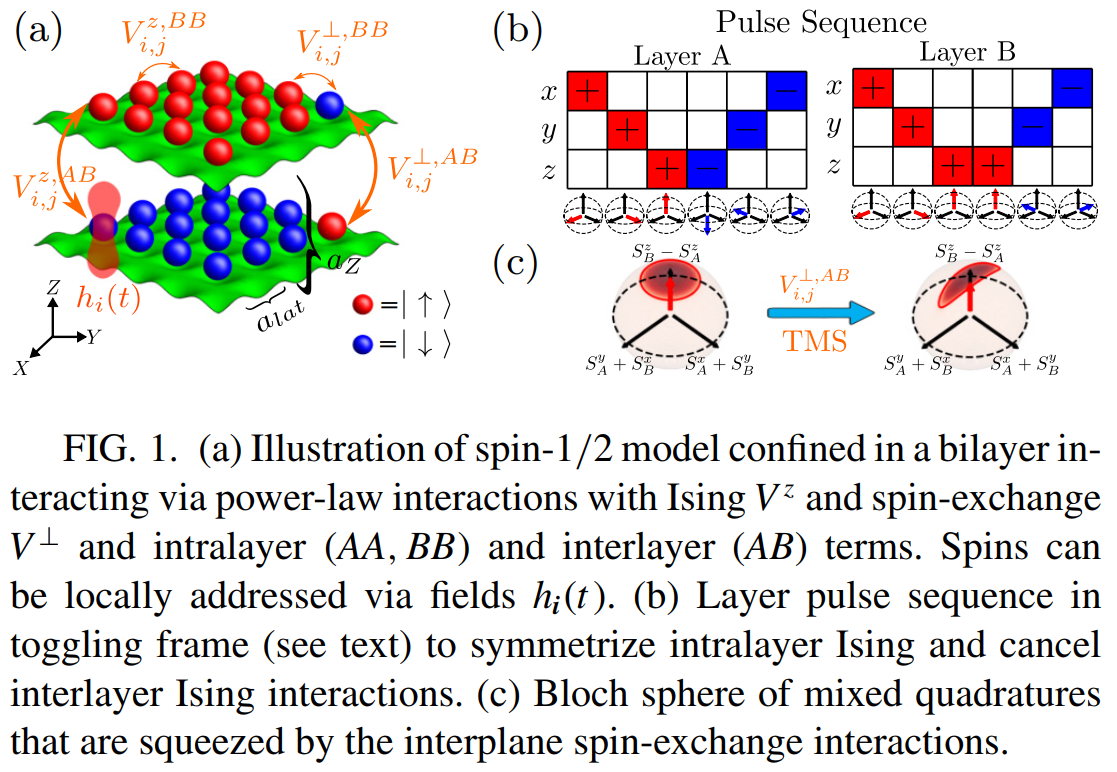
In classical sensing, the sensitivity of measurements improves with the number of particles or resources (such as photons or atoms) as 1/√N, known as the Standard Quantum Limit (SQL). However, quantum-enhanced sensing can leverage entangled states to surpass this limit and in principle achieve a scaling of 1/N, referred to as the Heisenberg limit, by maximizing the generation of metrologically useful 1entanglement. To that end, engineering the many-body dynamics of quantum systems to maximize the generation of useful entanglement is a critical goal for fulfilling the promise of quantum advantage. One particularly promising avenue is quantum spin systems, which can now be manipulated along the complementary axes of time and space, opening up new scopes for engineering their quantum dynamics.
In this work[1] with my supervisor Thomas Bilitewski, we show that combining spatial and temporal control enables Heisenberg-limited scaling of two-mode squeezing in power-law interacting spin models, currently accessible in a broad range of quantum platforms. Specifically, I work with a power-law interacting bilayer XXZ spin model, shown schematically in Fig. 1(a). The role of interlayer spin-exchange interactions ( V ⊥,AB ij ) in this model is to create entangled pairs of flipped spins, whereas the interlayer Ising interactions ( V z,AB ij ) will energetically penalize the creation of spin flips. We use Floquet pulse-sequence to engineer spin-spin interactions adapted to spatially structured states in bi-layers. This six-step layer-dependent sequence is shown in Fig. 1(b). This allows us to overcome limitations on the achievable squeezing, while also lifting restrictions on the required interactions, making it accessible in a broader range of platforms.
I performed extensive numerical calculations using a semiclassical phase-space method known as discrete truncated Wigner approximation (dTWA) to simulate the quantum many-body nonequilibrium dynamics of the spin model. I wrote my own Python scripts to model the appropriate bilayer and perform numerical integration and ran the scripts on an HPC cluster using bash scripts.
Our results demonstrate that Heisenberg scaling is achievable in this setting beyond the infinite range interaction case, opening it up to the full range of power-law interacting systems. Overall we show that using spatiotemporal control to engineer the many-body dynamics unlocks the ultimate limit of sensitivity in a variety of spin systems.

spin_squeezing

2.2 Universal Scaling of Two-mode Squeezing in Power-Law Interacting Spin Models

In our previous work discussed above, we showed that power-law interacting spin-1/2 XXZ models allow scalable generation of entanglement in the form of two-mode squeezing and thus achieves Heisenberg limited squeezing. Crucially, this depends on each spin layer behaving collectively, which requires sufficiently strong intra-plane and sufficiently homogeneous inter-layer interactions. In my current project with Thomas Bilitewski and in collaboration with our group’s postdoc Samuel Begg, I focus on the transition from dynamics characterized by Heisenberg limited squeezing to nonfully collective behavior in 1D (spin ladder) and 2D (spin bilayer) systems for a range of power-law interaction exponents. We identify a universal scaling of the generated squeezing in terms of system parameters and identify distinct phases as a function of dimensionality, power-law exponent, and aspect ratio of the system. We are currently at the manuscript preparation stage for this project. This study offers a comprehensive framework for engineering collective quantum states in experimental platforms that realize power-law spin models, advancing applications in quantum sensing and simulation.

3. Quantum Transport in Dirac Fermions

3.1 Phase transitions in topological material driven by scalar and mass disorder, uncovering rich transport behavior in 2D systems

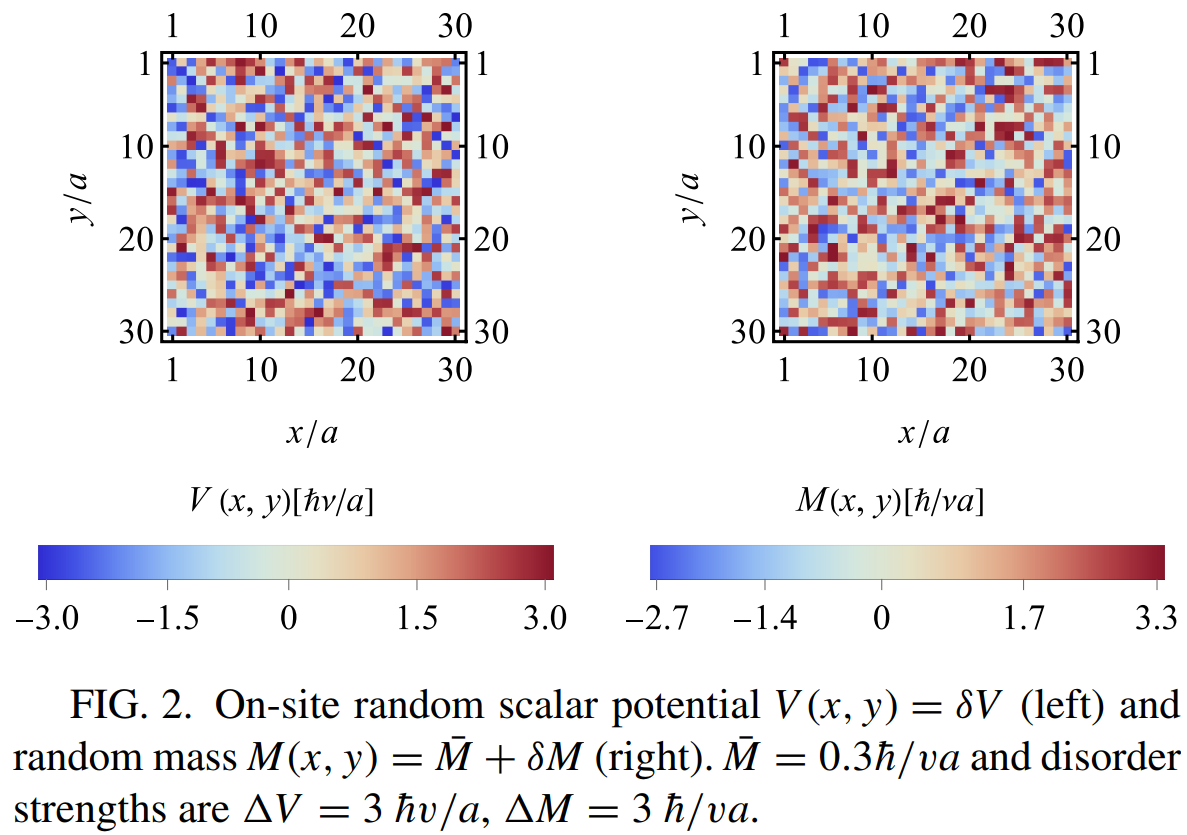
Two-dimensional Dirac fermions, particularly those found in topological materials, have promising applications in areas like spintronics, quantum computing, and optoelectronics due to robust surface conducting states with Dirac fermions that are protected against perturbations, allowing for highly efficient charge and spin transport with minimal dissipation. On the other hand, the unique nature of Dirac fermions can lead to unusual quantum transport phenomena, including quantized conductance and absence of metal-insulator transition under certain disorder types.
In this project, with my co-advisor Mario Borunda, I analyzed how the combination of scalar potential and mass disorder affects the transport properties of Dirac fermions. Using a tight-binding model on a lattice with uncorrelated on-site disorder, I calculated the conductivity from the transmission eigenvalues via the Landauer formula. For this, I wrote my own Mathematica scripts that model the lattice structure and calculate the eigenvalues.
Our results demonstrate that combining these two types of disorder leads to rich phase behavior, including insulating, scale-invariant, and metallic phases. The phases emerge at critical values of scalar potential and random mass (gap) disorder. Such disorders can be engineered by controlling the sample’s charge fluctuation which depends on the level of impurity. For multilayer systems like bilayer graphene or graphene on h-BN, the unprecedented precision in controlling twist angle and interlayer distance enables fine-tuning of interlayer coupling, which, along with gate voltage, determines the mass disorder.
Motivated by these experimentally realizable controls, I investigated a broad disorder landscape, identifying the critical disorder strengths at which the phase transitions occur. Our work highlights the interdependent way different types of disorders can affect the phases accessible to a massive Dirac fermion system and how tuning the disorders can control its transport behavior.

quantum_transport

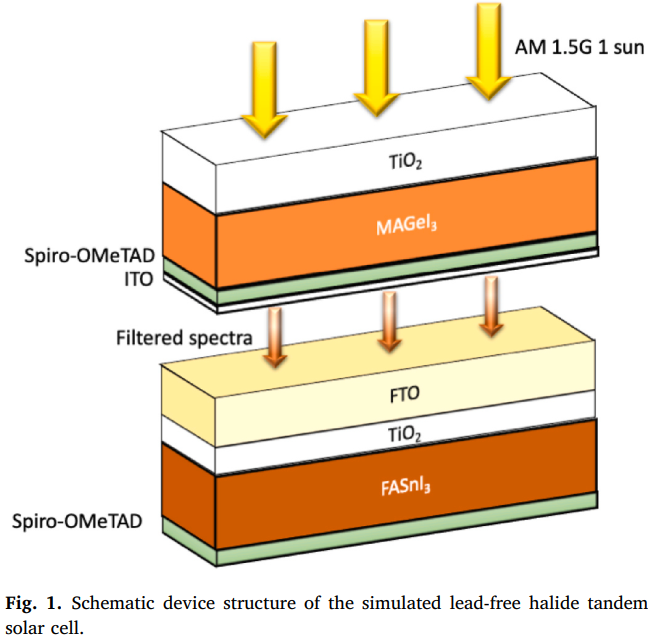
4. Lead-Free Perovskite Solar Cells

4.1 High-efficiency perovskite tandem solar cell, offering a sustainable alternative to lead-based designs

During the early stage of my Ph.D. before moving on to work with topological materials and spin models, I worked on numerically simulating solar cells and their optimization.
In this project[3] under the supervision of my co-advisor Mario Borunda, I used a numerical solar cell simulation tool, SCAPS, which solves the Poisson equation and the continuity equations for charge carriers (electrons and holes) to compute the electrostatics and transport properties within the solar cell. I modeled a tandem solar cell consisting of the perovskite subcells, MAGeI3 and FASnI3. Perovskite solar cells (PSCs) have gained significant attention in recent years due to their rapid efficiency improvements, cost-effectiveness, and versatility in parameter tuning. However, some of the best-performing perovskite materials contain lead, raising concerns about environmental impact and toxicity.
I addressed this challenge by working with lead-free perovskites and performing extensive numerical simulations to explore the parameter space of optoelectrical properties such as band gap, charge mobility, dielectric permittivity, etc. Our results show that after optimization, 31% efficiency is reached, suggesting lead-free perovskites can compete with lead-based devices.

solar_cell

Arman Duha